 |
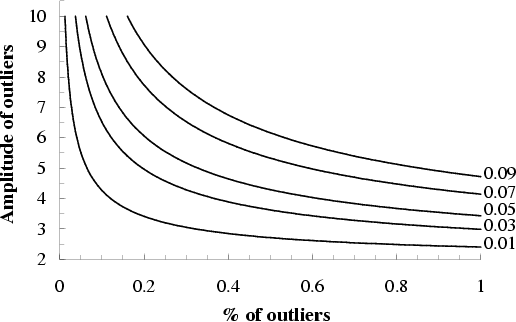
Outliers may affect the entropy values because they change the time series standard deviation and therefore, the value of the parameter r that defines the similarity criterion. Figure 4 shows that a small number of outliers with high amplitude has similar effects on the variance as a higher percentage of outliers with lower amplitude.
 |
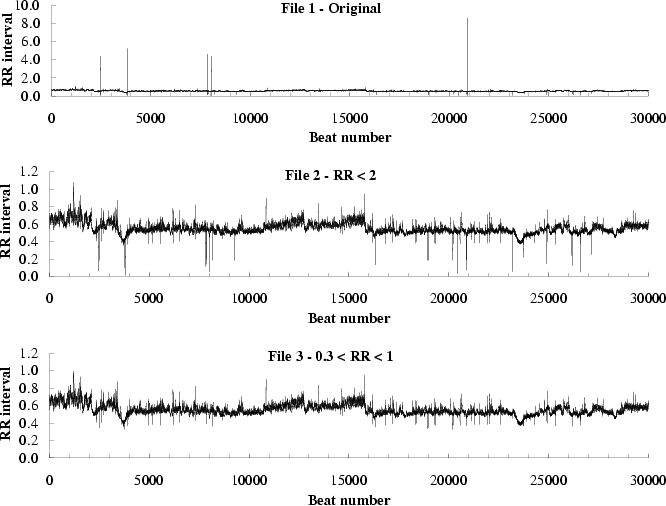
Figure 5 presents three RR interval time series derived from a 24 hour Holter recording of a healthy subject (nsr020). We calculate the MSE curves for a segment of the original time series (file 1) and two filtered time series (file 2 and file 3). File 1 contains the first 30,000 data points (RR intervals) of the original time series. File 2 contains the same data as file 1, but excluding the 6 RR intervals that exceed 2s. Similarly, file 3 contains these same intervals, but excluding the 43 RR intervals that are less than 0.3s or greater than 1s.
Using mse, we can obtain the following MSE analysis of these three files:
Scale File 1 File 2 File 3
1 0.009 0.734 0.734
3 0.012 0.937 0.933
5 0.012 1.137 1.140
7 0.011 1.138 1.144
9 0.011 1.222 1.210
11 0.011 1.174 1.224
13 0.011 1.204 1.186
15 0.011 1.199 1.186
17 0.010 1.183 1.189
19 0.009 1.186 1.212
File 1 includes 6 outliers (225.8, 4.43, 5.24, 4.65, 4.40, 8.61) at
least one order of magnitude higher than the mean value of the time
series. The sample deviations of the contents of files 1, 2 and 3 are
1.3, 0.62 and 0.60, respectively. For file 1, any two data points
![]() and
and ![]() such that
such that
![]() s are not
distinguishable. Therefore, this time series seems to be very regular
and the entropy values are close to zero. File 3 contains 37 fewer
outliers than file 2. However, since the difference between their
sample deviations is less than 0.05%, the entropy values are very
close. We note that the inclusion of a low percentage of outliers does
not significantly affect MSE analysis unless their differences from
the mean value of the time series are orders of magnitude larger than
the sample deviation.
s are not
distinguishable. Therefore, this time series seems to be very regular
and the entropy values are close to zero. File 3 contains 37 fewer
outliers than file 2. However, since the difference between their
sample deviations is less than 0.05%, the entropy values are very
close. We note that the inclusion of a low percentage of outliers does
not significantly affect MSE analysis unless their differences from
the mean value of the time series are orders of magnitude larger than
the sample deviation.
 |