

Next: MSE analysis of simulated white and 1/f noise
Up: Multiscale Entropy Analysis (MSE)
Previous: Multiscale Entropy Analysis (MSE)
Multiscale entropy (MSE) analysis [1,2] is a
new method of measuring the complexity of finite length time series. This
computational tool can be applied both to physical and physiologic
data sets, and can be used with a variety of measures of entropy. We
have developed and applied MSE for the analysis of physiologic time
series, for which we prefer to estimate entropy using the
sample
entropy
(SampEn)
measure [3]. SampEn is a refinement of the approximate
entropy family of statistics introduced by Pincus [4]. Both
have been widely used for the analysis of physiologic data
sets [5,6].
Traditional entropy measures quantify only the regularity
(predictability) of time series on a single scale. There is no
straightforward correspondence, however, between regularity and
complexity. Neither completely predictable (e.g., periodic) signals,
which have minimum entropy, nor completely unpredictable (e.g.,
uncorrelated random) signals, which have maximum entropy, are
truly complex, since they can be described very compactly. There is no
consensus definition of complexity. Intuitively, complexity is
associated with ``meaningful structural richness'' [7]
incorporating correlations over multiple spatio-temporal scales.
For example, we and others have observed that traditional single-scale
entropy estimates tend to yield lower entropy in time series of
physiologic data such as inter-beat (RR) interval series than in
surrogate series formed by shuffling the original physiologic data.
This happens because the shuffled data are more irregular and less
predictable than the original series, which typically contain
correlations at many time scales. The process of generating surrogate
data destroys the correlations and degrades the information content of the
original signal; if one supposes that greater entropy is
characteristic of greater complexity, such results are profoundly
misleading. The MSE method, in contrast, shows that the original
time series are more complex than the surrogate ones, by revealing
the dependence of entropy measures on
scale [8,9,10,11,12].
The MSE method incorporates two procedures:
- A ``coarse-graining'' process is applied to the time series. For a
given time series, multiple coarse-grained time series are constructed
by averaging the data points within non-overlapping windows of
increasing length,
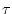 (see Figure 1). Each
element of the coarse-grained time series,
(see Figure 1). Each
element of the coarse-grained time series, 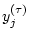 , is
calculated according to the equation:
, is
calculated according to the equation:
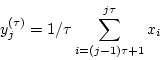 |
(1) |
where 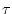 represents the scale factor and
represents the scale factor and
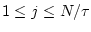 . The length of each coarse-grained time series is
. The length of each coarse-grained time series is
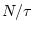 . For scale 1, the coarse-grained time series is simply the
original time series.
. For scale 1, the coarse-grained time series is simply the
original time series.
- SampEn is calculated for each coarse-grained time series, and then
plotted as a function of the scale factor. SampEn is a ``regularity
statistic.'' It ``looks for patterns'' in a time series and quantifies
its degree of predictability or regularity (see Figure 2).
Figure 1:
Schematic illustration of the
coarse-graining procedure for scale 2 and 3. Adapted from
reference [8].
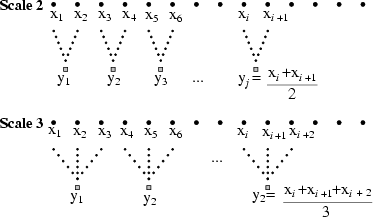 |
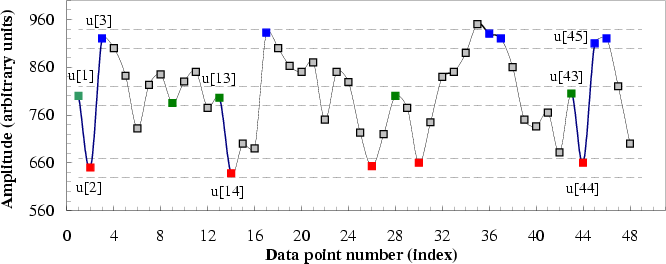
Figure 2:
A simulated time series u[1], ..., u[n] is
shown to illustrate the procedure for calculating sample entropy
(SampEn) for the case in which the pattern length, m, is 2, and
the similarity criterion, r, is 20. (r is a given positive
real value that is typically chosen to be between 10% and 20% of the
sample deviation of the time series.) Dotted horizontal lines around
data points u[1], u[2] and u[3] represent u[1] 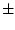 r,
u[2]
r,
u[2] 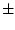 r, and u[3]
r, and u[3] 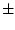 r, respectively. Two data
values match each other, that is, they are indistinguishable, if the
absolute difference between them is
r, respectively. Two data
values match each other, that is, they are indistinguishable, if the
absolute difference between them is 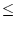 r. All green points
represent data points that match the data point u[1]. Similarly, all
red and blue points match the data points u[2] and u[3],
respectively. Consider the 2-component green-red template sequence
(u[1], u[2]) and the 3-component green-red-blue (u[1], u[2], u[3])
template sequence. For the segment shown, there are two green-red
sequences, (u[13], u[14]) and (u[43], u[44]), that match the template
sequence (u[1], u[2]) but only one green-red-blue sequence that
matches the template sequence (u[1], u[2], u[3]). Therefore, in this
case, the number of sequences matching the 2-component template
sequences is two and the number of sequences matching the 3-component
template sequence is 1. These calculations are repeated for the next
2-component and 3-component template sequence, which are, (u[2], u[3])
and (u[2], u[3], u[4]), respectively. The numbers of sequences that
match each of the 2- and 3-component template sequences are again
counted and added to the previous values. This procedure is then
repeated for all other possible template sequences, (u[3], u[4],
u[5]), ..., (u[N-2], u[N-1], u[N]), to determine the ratio between
the total number of 2-component template matches and the total number
of 3-component template matches. SampEn is the natural logarithm of
this ratio and reflects the probability that sequences that match each
other for the first two data points will also match for the next
point.
r. All green points
represent data points that match the data point u[1]. Similarly, all
red and blue points match the data points u[2] and u[3],
respectively. Consider the 2-component green-red template sequence
(u[1], u[2]) and the 3-component green-red-blue (u[1], u[2], u[3])
template sequence. For the segment shown, there are two green-red
sequences, (u[13], u[14]) and (u[43], u[44]), that match the template
sequence (u[1], u[2]) but only one green-red-blue sequence that
matches the template sequence (u[1], u[2], u[3]). Therefore, in this
case, the number of sequences matching the 2-component template
sequences is two and the number of sequences matching the 3-component
template sequence is 1. These calculations are repeated for the next
2-component and 3-component template sequence, which are, (u[2], u[3])
and (u[2], u[3], u[4]), respectively. The numbers of sequences that
match each of the 2- and 3-component template sequences are again
counted and added to the previous values. This procedure is then
repeated for all other possible template sequences, (u[3], u[4],
u[5]), ..., (u[N-2], u[N-1], u[N]), to determine the ratio between
the total number of 2-component template matches and the total number
of 3-component template matches. SampEn is the natural logarithm of
this ratio and reflects the probability that sequences that match each
other for the first two data points will also match for the next
point.
 |


Next: MSE analysis of simulated white and 1/f noise
Up: Multiscale Entropy Analysis (MSE)
Previous: Multiscale Entropy Analysis (MSE)
Madalena Costa (mcosta@fas.harvard.edu)
2005-06-24

